Problemas con sumas y restas

Ana Lozano Alonso

Errores más frecuentes en los algoritmos de la suma y la resta

v  Colocación de los números.

v  Orden: empiezan a sumar o restar por la columna de la izquierda y avanza hacia la derecha.

v  Resta de la cifra menor de la mayor aunque ésta esté en el sustraendo.

v  Colocación de un cero en el resultado cuando la cifra del sustraendo es mayor que la del minuendo.

v  Equivocaciones en los resultados de las sumas o restas de cada columna.

v  Escritura del resultado completo.

v  Olvido de la llevada.

Ana Lozano Alonso

ABN en restas

Hoy en clase primeramente hemos realizado una ficha en la cual hemos expuesto los aspectos positivos de la asignatura, los negativos, sugerencias y recomendaciones a nuestro profesor, y una introspección.
También hemos realizado un problema del test de autoevaluación del campus virtual, concretamente el de la capacidad del deposito de gasolina de un coche.
Y por ultimo hemos hecho algunos ejemplos de algoritmos basados en números (ABN), de restas y con ello hemos aprendido que se tiene que quitar la misma cantidad (la que se quiera) del minuendo y del sustraendo, hasta conseguir cero en el sustraendo.

NOTA: una web de interes para realizar este tipo de algoritmos es algorismosabn.com

REALIZADO POR: Jennifer Viejo Hidalgo y Eva Carreras Teruel.

La resta

-          Concepto de resta

En sentido matemático y al contrario que las suma, la resta es una operación que no puede ser definida dentro del conjunto de los números naturales, ya que siempre se puede hacer la suma de dos números cualquiera, pero no ocurre lo mismo con la resta. La resta se suele definir como la operación inversa de la suma.

Las situaciones que se representan mediante la resta corresponden a dos tipos:

·         Quitar de una cantidad y observar lo que queda.

·         Calcular cuánto falta a una cantidad para igualarse a otra.

Los problemas asociados con la operación de resta estarían relacionados con:

Ø  Hallar el resto de la operación.

Ø  Búsqueda de sumandos complementarios (se busca lo que falta aun sumando para igualarse a otro).

Ø  Comparación de medidas.

-          Enseñanza del algoritmo de la resta

RESTA CON NÚMEROS DE UNA CIFRA

Es la base para el aprendizaje de la resta con números de varias cifras.

El aprendizaje de la resta pasa por tres fases: la misma operación se puede hacer de varias maneras, hasta alcanzar la base para el cálculo mental. Todos los alumnos tienen que pasar por estas fases. Son las siguientes:

1.       Quitar o separar de: es la estrategia más elemental y supone un adecuado dominio del conteo regresivo de números.

2.       Contar hacia atrás: se parte de la cantidad inicial para contar hacia atrás tantos números como sea la cantidad de cambio realizado.

3.       Contar hacia delante las que faltan: esta estrategia es la más útil. El objetivo último es que los alumnos comprendan que la resta es el opuesto de la suma y que restar no es más que calcular el complementario de una cantidad hasta alcanzar otra.

RESTA CON NÚMEROS DE VARIAS CIFRAS

Vamos a distinguir dos fases:

o   Restas sin compensación delos órdenes inmediatos superiores (restas “restas sin llevarse”).

o   Restas con compensación de uno o varios órdenes.

Distinguiremos varios casos distintos según el nivel de dificultad:

§  Una sola compensación de orden: compensación de orden en las unidades sin y con cero en el minuendo.

§  Compensación de orden en las decenas sin y con cero en las decenas.

§  Varias compensaciones de orden: sin ceros en el minuendo.

Ana Lozano Alonso

La suma

-          Concepto de suma

Si tenemos dos conjuntos disyuntivos cuyos cardinales vienen representados por dos números A y B, la suma de estos dos números sería el cardinal del conjunto, es decir, la unión de los dos conjuntos.

Las situaciones que se representan mediante la adición corresponden a dos tipos:

·         Situaciones de agrupar, reunir, juntar…

·         Situaciones de aumentar, agregar o añadir a algo que ya existe.

-          Enseñanza del algoritmo de la suma

SUMA CON NÚMEROS DE UNA CIFRA

Es la base de todo el posterior aprendizaje de la suma. El objetivo será el conocimiento y recuento automático de todas las combinaciones de sumas de números de números de una cifra (tablas de sumar).

Para ello se debe pasar por una serie de etapas: primero  se hace con objetos reales, después con objetos que representan otros y finalmente utilizando las palabras (números) que también tienen la función de representar. Todas estas etapas son de recuento verbal, por lo que deben desarrollarse antes de proceder al cálculo escrito:

·         Conteo de todos los elementos: el niño representa las dos colecciones de objetos a sumar mediante algún tipo de material, luego los junta y y vuelve a contar el conjunto.

·         Conteo a partir del primer sumando: el niño nombra el primer sumando y continúa contando la colección de objetos que representa al segundo sumando.

·         Conteo a partir del sumando mayor: igual que el caso anterior, pero eligiendo como primer sumando el número mayor.

Es muy importante trabajar desde un principio las propiedades de la adición por el hecho de su utilidad en el cálculo, sobre todo en el mental.

a.       Propiedad conmutativa: el orden en que se consideran dos sumandos no modifica su suma.

b.      Propiedad asociativa: si hay más de dos sumandos, el orden en que se sumen es indiferente: el resultado siempre es el mismo.

c.       Propiedad disociativa: es igual que la anterior, pero a la inversa. Todo sumando puede descomponerse en partes o sumandos menores de la forma que se quiera siempre que su suma equivalga al sumando inicial.

d.      Existencia de un elemento neutro: que es el 0. Cuando se suma a una cantidad ésta no varía. Esto rompe la falsa creencia de que sumar dos números siempre da lugar a un resultado mayor que ambos sumandos.

SUMA CON NÚMEROS DE VARIAS CIFRAS

Vamos a distinguir dos fases:

o   Sumas sin compensación de los órdenes inmediatos superiores (suma “sin llevarse”).

o   Sumas con compensación de uno o varios órdenes (suma “llevándose”).

Ana Lozano Alonso

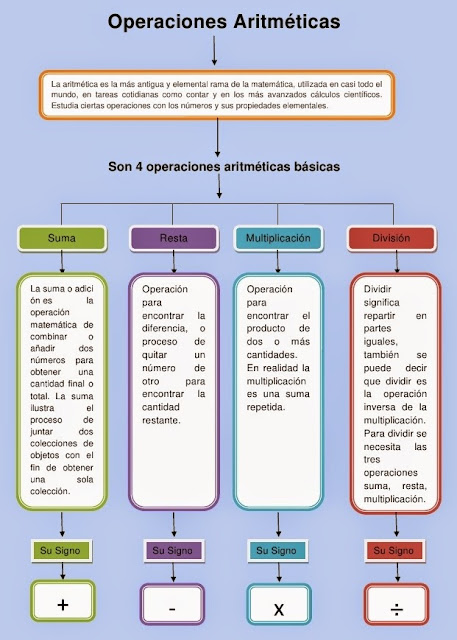
Las operaciones aritméticas

1.       Concepto de operación

Una operación es una acción interiorizada, un proceso mediante el cual se realiza mentalmente la manipulación de una acción real.

Hablamos de operaciones matemáticas si la operación manipulativa se sustituye por una operación simbólica que nos da el resultado sin necesidad de realizar la acción. La operación simbólica es una forma más cómoda de resolver el problema y además útil, ya que en muchos casos no se podría realizar la acción real. No obstante, la manipulación de objeto es la fase anterior a las operaciones aritméticas con números.

2.       Etapas en el aprendizaje de las operaciones.

A.      PRIMERA ETAPA: Etapa manipulativa

El alumno toca los materiales y realiza las operaciones manualmente. Los problemas puedes escenificarse para resolverse.

B.      SEGUNDA ETAPA: Etapa verbal

El alumno desarrolla la competencia en comunicación lingüística debido a que debe incorporar a su lenguaje habitual lo básico del lenguaje matemático. Además, también sirve para fomentar la competencia matemática en sí misma.

Se compone de dos fases:

-          Relato de la acción: El alumno relata lo que está haciendo. Lenguaje y acción se complementan mutuamente.

-          Resumen oral de la acción: El alumno, una vez acabada la actividad, cuenta el desarrollo del ejercicio realizado de forma verbal, de manera que así desarrolla su capacidad para organizar y resumir. Importante la capacidad metacognitiva.

C.      TERCERA ETAPA: Etapa gráfica

El alumno representa mediante dibujos las operaciones realizadas, ya sea la acción manipulativa en sí o los materiales empleados.

D.      CUARTA ETAPA: Etapa simbólica

El alumno representa y realiza las operaciones mediante símbolos. También aprende los algoritmos de resolución de operaciones.

En todas las etapas debe estar presente la manipulación oral, ya que se trata de lo más importante de todo.

3.       Principios metodológicos en la enseñanza de las operaciones

1.       Las operaciones deben ser enseñadas y trabajadas dentro de un contexto de resolución de problemas.

Es fundamental transmitir a los niños que las operaciones son una manera de solucionar problemas reales para lo cual necesitamos emplear diferentes estrategias. Las operaciones son una manera de resolver problemas sin necesidad de manipular sus elementos reales.

Es muy importante no basarnos nunca en enseñar las operaciones de forma aislada, mecanizarlas y luego centrarlas en resolver problemas. Esta metodología hace concebir al alumno que las operaciones son una técnica o un instrumento para resolver los problemas y no al revés.

Las situaciones que se trabajen en los problemas deben ser variadas paraquelos alumnos puedan utilizar las distintas tipologías de problemas y para evitar que los alumnos identifiquen los problemas como un texto en el que, con los númerosque aparecen en el enunciado, hay que hacer una cuenta de sumar o de restar en función de la palabra clave que aparezca.

2.       Hay que comprender lo que se hace y luego mecanizarlo.

Los alumnos que comprendan la operación de manera manipulativa comprenderán mejor la operación de forma simbólica. Así, gracias a que comprende y reconoce los pasos a seguir podrá buscar las causas de su error cuando el resultado no sea el requerido y corregir de forma autónoma sus propios errores.

3.       Se deben utilizar distintas formas para el aprendizaje de los conceptos de las operaciones y de sus algoritmos.

Tendremos que tener en cuenta los principios de la variabilidad matemática y perceptiva: un mismo concepto puede ser abordado desde distintos enfoques. Es muy importante que cualquier concepto matemático sea presentado dedistintas formas y en distintos contextos, para lograr la integración entre todas las formas de presentación del mismo concepto.

4.       Mecanización de las operaciones.

Significa que el niño adquiera rapidez y sea capaz de automatizar los pasos a realizar en los distintos algoritmos para que pueda utilizarlos convenientemente en las operaciones que sean necesarias. Para evitar caer en la rutina es imprescindible que exista variedad en la presentación de situaciones y gradualidad en la dificultad de actividades.

5.       Primero cálculo oral y después cálculo escrito.

La primera tarea que deben los alumnos realizar ante una operación es la de observar y leer los términos con el fin de estimar el resultado, ya que el cálculo oral se convertirá después en el cálculo mental, así como el cálculo escrito debe servir para afinar el proceso del cálculo mental.

A lo largo de este viaje por el universo de las matemáticas nos iremos adentrando en las cuatro operaciones aritméticas básicas: suma, resta, multiplicación y división:

Ana Lozano Alonso

¿Qué es un conjunto?

La clase de hoy ha sido más distendida, saliéndose de lo habitual. Hemos realizado un ejercicio práctico en los jardines de la Universidad para probar distintas formas de transmitir a los alumnos el concepto de conjunto.
Para ello nos hemos ido organizando en función de un rasgo predominante, por ejemplo, quién realizaba alguna actividad física. Hemos comprobado que esto sería una buena forma de averiguar cosas de nuestros alumnos sin preguntarles directamente, o incluso de hacer actividades de grupo que rompiesen el hielo los primeros días.
Esta actividad más dinámica nos ha acercado un poco más a las matemáticas, dándonos otra visión de éstas. Pensamos que podríamos realizar más a menudo este tipo de actividades.

En matemáticas, un conjunto es una colección de elementos considerada en sí misma como un objeto. Los elementos de un conjunto pueden ser cualquier cosa: personas, números, colores, letras, figuras, etc. Se dice que un elemento (o miembro) pertenece al conjunto si está definido como incluido de algún modo dentro de él.

Ejemplo: el conjunto de los colores del arcoíris es:

AI = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta}

Un conjunto suele definirse mediante una propiedad que todos sus elementos poseen. Por ejemplo, para los números naturales, si se considera la propiedad de ser un número primo, el conjunto de los números primos es:

P = {2, 3, 5, 7, 11, 13, ...}

Un conjunto queda definido únicamente por sus miembros y por nada más. En particular, un conjunto puede escribirse como una lista de elementos, pero cambiar el orden de dicha lista o añadir elementos repetidos no define un conjunto nuevo. Por ejemplo:

S = {Lunes, Martes, Miércoles, Jueves, Viernes} 

   = {Martes, Viernes, Jueves, Lunes, Miércoles}

AI = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta} 

     = {Amarillo, Naranja, Rojo, Verde, Violeta, Añil, Azul}

Los conjuntos pueden ser finitos o infinitos. El conjunto de los números naturales es infinito, pero el conjunto de los planetas en el Sistema Solar es finito (tiene ocho elementos). Además, los conjuntos pueden combinarse mediante operaciones, de manera similar a las operaciones con números.

Los conjuntos son un concepto primitivo, en el sentido de que no es posible definirlos en términos de nociones más elementales, por lo que su estudio puede realizarse de manera informal, apelando a la intuición y a la lógica. Por otro lado, son el concepto fundamental de la matemática: mediante ellos puede formularse el resto de objetos matemáticos, como los números y las funciones, entre otros.

Ana Lozano Alonso

Los números naturales y los sistemas de numeración

Las matemáticas son una ciencia que está en uso constante y ha ido evolucionando a lo largo del tiempo debido al cambio que se ha constatado a lo largo de los siglos y los distintos tipos de sociedades. Esto puede guardar relación con lo que va aprendiendo el niño a lo largo de los años, pues pasa de lo concreto a lo abstracto.

Para satisfacer las necesidades surgidas a lo largo de la evolución surgen las técnicas de recuento, y el elemento que todas tienen en común es  el conjunto de objetos que se quiere contar es puesto en correspondencia con otro conjunto de objetos. Para salvar los errores del conteo es fundamental el aprendizaje temprano de la serie numérica, algo que los niños hacen de forma natural así como el uso de técnicas auxiliares.

En el tema 2 hemos visto también los principios generales de las técnicas de recuento, la ordenación de los números según sean cardinales u ordinales, la utilización avanzada de las técnicas de conteo (las cuales tienen importancia para una realización eficaz de las operaciones aritméticas. Los alumnos pasan por distintas fases en el aprendizaje de estas técnicas, avanzando cada vez un poco más. El concepto de número, los sistemas de numeración (es distinto según sea una sociedad primitiva o una sociedad más avanzada)  pero en todos los sistemas de numeración existen dos conceptos fundamentales: uno es el concepto de “orden” de las unidades. El otro concepto básico es el de “base” Se llama “base” al número de unidades de un orden que se deben repetir para pasar a formar una unidad de orden superior. Gran parte de la dificultad de los niños al aprender el sistema de numeración, es que tienen que aprender dos sistemas: el oral y el escrito. Tipos de sistemas de numeración escrito: existen 3 tipos de numeración: 
- Aditivo regular
- Multiplicativo regular
- Posicional regular: (Este sistema traído a Europa por los árabes, es el origen de nuestro sistema de numeración que actualmente utilizamos, y que sustituyó al sistema al sistema de numeración romana).

- Los cambios de base de numeración: Para pasar números entre dos bases distintas del decimal, lo más sencillo es pasarlo previamente a ésta, utilizándola como base intermedia.

- Los números romanos: Su origen está en señales hechas para indicar grupos de objetos y fueron sustituidos por letras debido a su parecido.

Los símbolos I (uno), X (diez), C (cien) y M (mil) son los ‘principales' y los símbolos V (cinco), L (cincuenta) y D (quinientos) los 'secundarios' Los símbolos principales no se pueden repetir más de tres veces y los secundarios no pueden repetirse ninguna vez. - Todo símbolo situado a la derecha de uno de igual o mayor valor se suma. Si un símbolo principal está situado a la izquierda de un símbolo de mayor valor se resta. - A la izquierda de un símbolo solo se puede poner como símbolo de menor valor el símbolo principal inmediatamente anterior. 5.- Los millares, diez millares, cien millares, etc. de los números mayores o iguales que 4.000 se escriben como si fueran unidades, decenas, centenas, etc., colocándoles una raya horizontal por encima.

- Materiales para el estudio de la numeración: modelos proporcionales, modelos no proporcionales,  dinero, fichas de colores…etc.

Eva Carreras Teruel